"A calculator app? Anyone could make that." Not true. A calculator should show you the result of the mathematical expression you entered. That's much, much harder than it sounds. What I'm about to tell you is the greatest calculator app development story ever told.
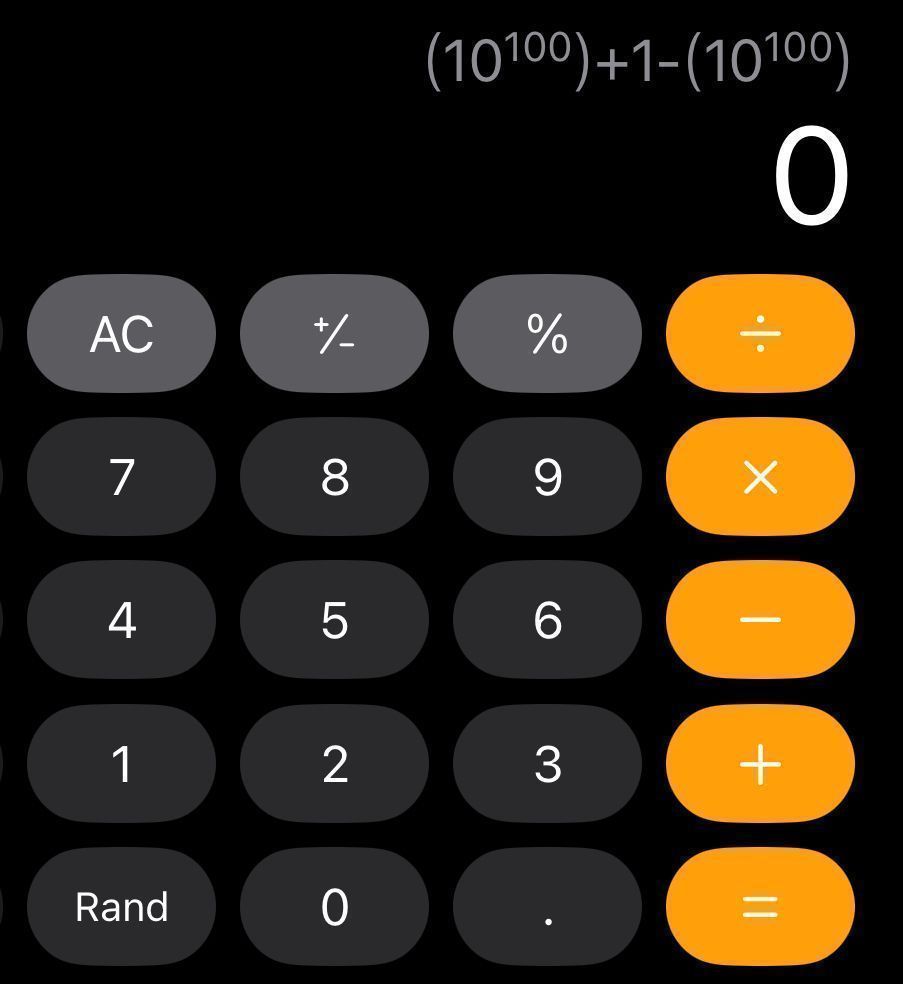
That picture is from iOS calculator. Notice anything? It's wrong. (10^100) + 1 − (10^100) is 0, not 1. Android gets it right. And the story for how is absolutely insane.
Google hired Hans-J. Boehm, of the "Boehm garbage collector" fame. They needed an elite coder to fix garbage collection and concurrent programming. He led the effort to define C++ shared variable semantics. But then they gave him an impossible task: write a calculator app.


Even for him, this must have been a challenge. The purpose of a calculator app is to give you correct answers. Floating point numbers are imprecise - they cannot represent 0.3 or 10^100. This means a calculator built on floating point numbers is like a house built on sand.
It bears repeating. To give correct answers to mathematical expressions, a calculator must represent numbers. And almost all numbers cannot be expressed in IEEE floating points. Even simple operations with floating point numbers requires careful thought for an accurate answer

Some problems can be avoided if you use bignums. Most numeric types are always 2 or 4 bytes. Not so for bignums. These are integers without bounds. They grow in memory as needed. This solves the (10^100) + 1 - (10^100) example. But bignums are integers. How about fractions?

Fractions can be solved easily. Just use bignums for the numerator and denominator. The implementation of arithmetic ops on such a type are trivial, and will always give exact answers. This is where many would have declared victory. But Boehm wasn't satisfied. Not even close.
Math goes much deeper than fractions. What about π or √2? A calculator that is based on arbitrary-precision fractions still can't tell you the circumference of a circle, since π is not expressible as a fraction. If your calculator can't handle 9th grade math, what good is it?
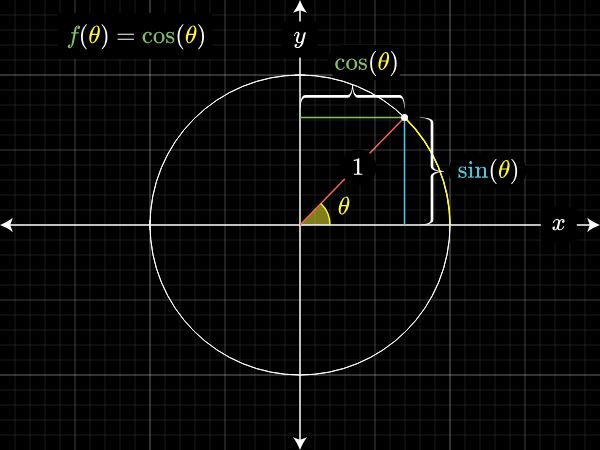
Algebraic arithmetic would get him closer. Forget about representing numbers as numerators and denominators. You can represent them as the polynomial equation they satisfy. For √2, it would be x² - 2 = 0. (Plus you'd store that you want the positive root.)
Now math ops get a little trickier to implement: - To add, you create a new polynomial that has their sum as a root - To multiply, you use polynomial composition and resultants Guess what? Still not good enough for Boehm. This only works for algebraic numbers. Doesn't get us π
So Boehm had no choice but to go even deeper. It was time to get serious. We started off with integers (bignum), went to rational numbers, then algebraic numbers. What's next? Constructive real numbers.
So Boehm began to consider "recursive real arithmetic" (RRA). Given an expression and how precise you want the answer, RRA gives you an answer at least that precise. Check out the cover of this classic textbook. See how the rulers get smaller and smaller?

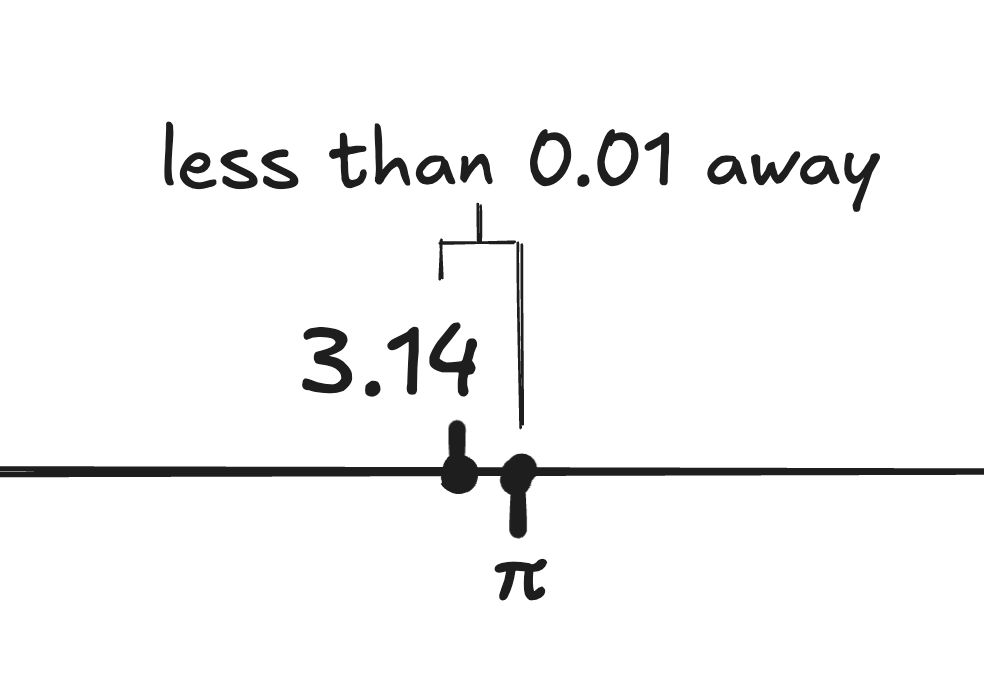
Constructive real numbers are those numbers that you can compute more and more accurately. You can't ever tell me all the decimals of π. But if I ask for a rational number within 0.01 of π, you can tell me 3.14. π is within 0.01 of 3.14, so that's a valid answer.
Now let's say I ask for a number within 0.01 of 2π. You know how to generate digits of π. (3.14159...) You can then take some of them and multiply that by 2. But how many digits do you need to take, to make sure your answer is within 0.01 of 2π?
Multiplying a number by 2 doubles the error. I asked for 2π to within 0.01 decimals, so you need an approximation of π that's within 0.005 decimals. Let's say you come up with 3.141, which is indeed less than 0.005 away from π. Multiply that by 2 and you're done!
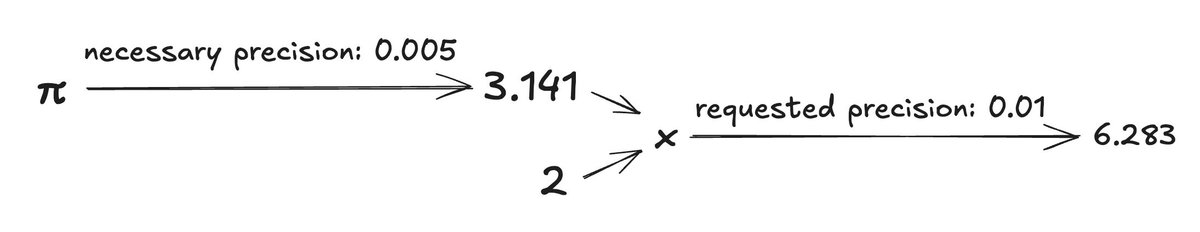
RRA works this way. Every number in RRA is represented as a function that takes a rational and returns a rational. The rational it takes is the requested tolerance. The rational it returns is guaranteed to be within that tolerance of the real number it represents

This means RRA is simple to use. You say how precise the answer must be, and it recursively figures out how much precision is needed in all the intermediate calculations. It can handle expressions involving π or √2 without a problem. Essential for a calculator.
You're thinking "Surely Boehm stopped here". Just set the "output precision" to be the number of digits displayed by the calculator, right? Then all the digits displayed by the calculator would be correct. So now the calculator always shows the correct answer! Right?

But not so fast. When users type "1-1", the answer is 0, so you want to show "0". But RRA will only tell you "1-1 is within a rounding error of 0.0000000000000" Showing 0.0000000000000 on the screen, when the answer is exactly 0, would be a horrible user experience.
Boehm was back to the drawing board. At this point he must have been concerned. His "space efficient conservative garbage collection" was child's play compared to this. He couldn't do it alone. He recruited colleagues such as Corky Cartwright and Vernon Lee Jr to help

You can check that two RRA numbers are *not* equal. You can compute them with more and more accuracy until you see where they differ. But if the numbers are equal, you'll just be computing them with more and more accuracy forever. It doesn't terminate.
Remember - if the calculator showed 0 for e^(-10000), that would be wrong. It's not 0. It should say 0.00000... and let you scroll until you see where it changes But, it SHOULD show 0 when you type sin(π). sin(π) is exactly 0 RRA gives us no way to tell that sin(π) is exactly 0
Or you could just not give an answer at all, like the iOS calculator does lol

So showing an exact answer is impossible to solve with constructive real numbers. But Boehm and co had a realization. They don't need to work with all constructive real numbers They only need to work with the numbers you can express with the operations available on a calculator
These are: 1. The four basic arithmetic operations, and square roots. 2. The sin, cos, and tan trigonometric functions and their inverses. 3. Exponential and (natural) logarithm functions
This is a much smaller set of numbers than all constructive reals. And in fact, someone had already researched this exact problem. Their names were Dan Richardson and John Fitch, and they solved it in 1994.

Their solution is absolutely correct. Unless one of the numbers is a counterexample to Shanuel’s conjecture. But realistically, that's not going to happen. Schanuel's conjecture is one of the most important in number theory, and no one has found a counterexample yet

It sounds perfect. But there's just one problem. It's too slow. 1 is not equal to 1 - e^(e^(-1000)). But for Richardson and Fitch's algorithm to detect that, it would require more steps than there are atoms in the universe. They needed something faster.
Their original problem was to see if two constructive real numbers were equal. That was impossible to solve. They simplified it and got closer, by limiting how they could construct the numbers. That made the problem solvable, just slow. Could they simplify it again?
They realized that it's not the end of the world if they show "0.000000..." in a case where the answer is exactly 0, although it's not the ideal UX. They just can't show "0" in a case where the answer is 0.0000001. Maybe a faster, conservative algorithm was possible?
Then they came up with something truly brilliant. RRA gives you the full power of the constructive real numbers, with the drawback that getting exact answers becomes impossible. Rational arithmetic gives exact answers, but can't express π. Could their strengths be combined?



